Pythonで1次遅れ系のステップ応答をプロットする方法

制御工学において、1次遅れ系のステップ応答は非常に重要です。
今回はPythonのcontrol system libraryを使って、1次遅れ系のステップ応答をプロットする方法を紹介します。
ライブラリを使わずにプロットする方法も紹介します。

1次遅れ系のステップ応答の理論
ステップ応答のプロット
control system library を使った実装
まとめ

1次遅れ系のステップ応答の理論

1次遅れ系は、制御工学においてよく使用される伝達関数の一つで、以下の特徴を持ちます。

入力信号がステップ関数の場合、出力信号は指数関数的に立ち上がる
時間が経過するにつれて出力信号は入力信号に漸近的に追従する
伝達関数は、分母が1次式、分子が定数の比で表される

ステップ応答のプロット

ライブラリを使わないプロット

import numpy as np
import matplotlib.pyplot as plt

K = 1.0  # ゲイン
T = 2.0  # 時定数

# 応答の時間範囲を指定
t = np.linspace(0, 10, 1000)

# ステップ入力信号の定義
u = np.ones_like(t)

# 1次遅れ応答の計算
y = K * (1 - np.exp(-t/T))

# グラフのプロット
plt.plot(t, u, 'b-', label='Step Input')
plt.plot(t, y, 'r-', label='Step Response')
plt.xlabel('Time (sec)')
plt.ylabel('Amplitude')
plt.title('Step Response of First-Order System')
plt.legend()
plt.grid()
plt.show()

結果は以下の通りです。

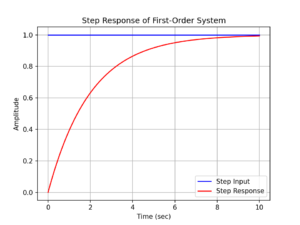
control system library を使った実装

control system library の概要と特徴の説明
1次遅れ系の伝達関数の定義方法の説明
control system library を用いたステップ応答の計算方法の説明

control system libraryを使ったプロット

import numpy as np
import matplotlib.pyplot as plt
import control

K = 1  # ゲイン
T = 2  # 時定数

# 応答の時間範囲を指定
t1 = np.linspace(0, 14, 1000)

# ステップ入力信号の定義
u = np.ones_like(t1)

# 1次遅れ応答の計算
y = K * (1 - np.exp(-t1/T))

#cotrol system library で実装
num = np.array([K])
den = np.array([T, 1])

H = control.tf(num, den)
print('H(s) =', H)

t2, y2 = control.step_response(H)

# グラフのプロット
plt.plot(t1, u, 'b-', label='Step Input')
plt.plot(t1, y, 'r-', label='Step Response')
plt.plot(t2, y2, 'g-', label='cotrol system library')
plt.xlabel('Time (sec)')
plt.ylabel('Amplitude')
plt.title('Step Response of First-Order System')
plt.legend()
plt.grid()
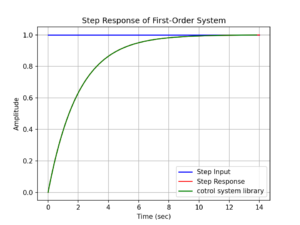
plt.show()

結果は以下の通りです。
ライブラリを用いた結果（緑）とライブラリを用いない結果（赤）が重なり、同じ結果になっていることが確認できます。